A. Relasi dan Fungsi
1. Relasi Relasi dapat dipahami dalam banyak hal di kehidupan sehari-hari. Konsep relasi menjelaskan hubungan antara anggota-anggota dari dua himpunan. Contohnya, setiap pemain bola di tim Manchester United memiliki nomor punggung masing-masing.
 Hubungan ini biasanya dijelaskan dalam bentuk himpunan pasangan berurut, diagram panah, dan diagram Kartesius.
a. Himpunan Pasangan Berurut
MU = {(Sancho, 25), (Rashford, 10), (Shaw, 23)}
b. Diagram Panah
Hubungan ini biasanya dijelaskan dalam bentuk himpunan pasangan berurut, diagram panah, dan diagram Kartesius.
a. Himpunan Pasangan Berurut
MU = {(Sancho, 25), (Rashford, 10), (Shaw, 23)}
b. Diagram Panah
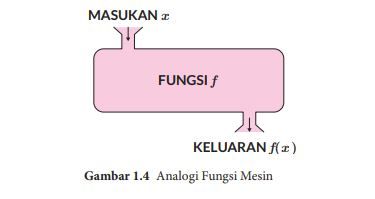 Fungsi merupakan suatu relasi yang menghubungkan satu anggota dari suatu
himpunan tepat ke satu anggota di himpunan yang lain. Fungsi adalah relasi yang
lebih spesifik. Fungsi biasa dinyatakan dalam bentuk f(x) = y , di mana f merupakan fungsi, x merupakan variabel masukan (input) dan y adalah variabel keluaran output. Kita dapat memahami konsep ini dengan membayangkan fungsi sebagai mesin seperti pada gambar diatas.
a. Fungsi dan Bukan Fungsi
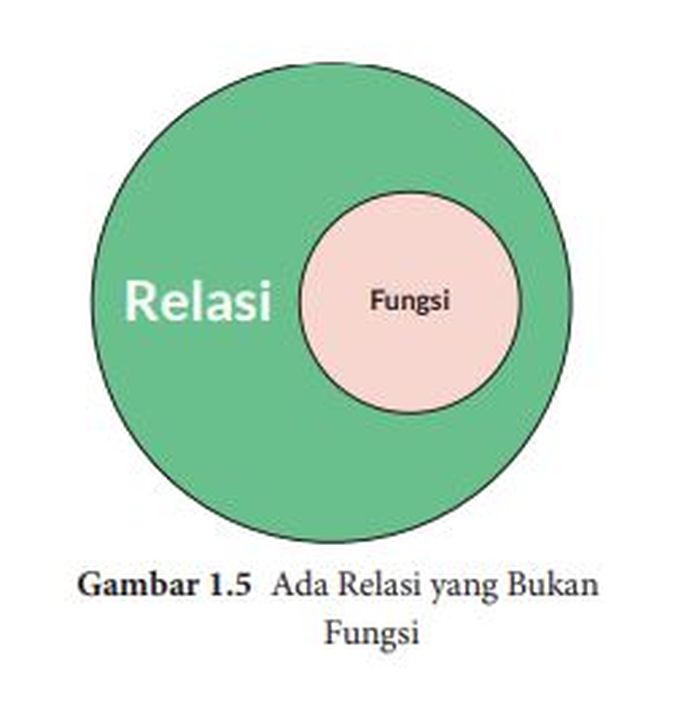
Secara ilustratif, hubungan antara fungsi dan relasi dapat dipahami melalui gambar berikut:
Fungsi merupakan suatu relasi yang menghubungkan satu anggota dari suatu
himpunan tepat ke satu anggota di himpunan yang lain. Fungsi adalah relasi yang
lebih spesifik. Fungsi biasa dinyatakan dalam bentuk f(x) = y , di mana f merupakan fungsi, x merupakan variabel masukan (input) dan y adalah variabel keluaran output. Kita dapat memahami konsep ini dengan membayangkan fungsi sebagai mesin seperti pada gambar diatas.
a. Fungsi dan Bukan Fungsi
Secara ilustratif, hubungan antara fungsi dan relasi dapat dipahami melalui gambar berikut:
 1) Perhatikan pasangan berurut berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
i) {(1,2),(2,3),(3,4),(4,5)} → Relasi : Fungsi
ii) {(1,3),(1,4),(2,3),(3,4)} → Bukan Fungsi
iii) {(2,3),(3,3),(4,3),(5,3)} → Relasi : Fungsi
iv) {(5,1),(6,2),(7,3),(5,4)} → Bukan Fungsi
2) Perhatikan diagram panah berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
1) Perhatikan pasangan berurut berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
i) {(1,2),(2,3),(3,4),(4,5)} → Relasi : Fungsi
ii) {(1,3),(1,4),(2,3),(3,4)} → Bukan Fungsi
iii) {(2,3),(3,3),(4,3),(5,3)} → Relasi : Fungsi
iv) {(5,1),(6,2),(7,3),(5,4)} → Bukan Fungsi
2) Perhatikan diagram panah berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
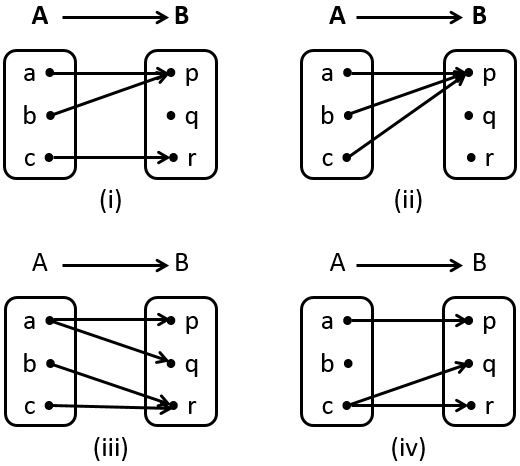 (i) Relasi : Fungsi
(ii) Relasi : Fungsi
(iii) Relasi : Bukan Fungsi
(iv) Relasi : Bukan Fungsi
3) Perhatikan diagram kartesius berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
i) Relasi : Fungsi
(ii) Relasi : Bukan Fungsi
(iii) Relasi : Fungsi
(iv) Relasi : Bukan Fungsi
Untuk menentukan diagram kartesius tersebut apakah relasi : fungsi atau bukan , kita dapat menggunakan Tes Garis Vertikal. Caranya yaitu cukup menggeser garis vertikal dari kiri ke kanan (atau sebaliknya) dan melewati garis relasi. Apabila garis vertikal tersebut memotong grafik di dua atau lebih titik yang berbeda, maka relasi tersebut bukanlah fungsi.
(i) Relasi : Fungsi
(ii) Relasi : Fungsi
(iii) Relasi : Bukan Fungsi
(iv) Relasi : Bukan Fungsi
3) Perhatikan diagram kartesius berikut! Ada yang menunjukkan relasi yang berupa fungsi dan ada yang menunjukkan relasi yang bukan fungsi.
i) Relasi : Fungsi
(ii) Relasi : Bukan Fungsi
(iii) Relasi : Fungsi
(iv) Relasi : Bukan Fungsi
Untuk menentukan diagram kartesius tersebut apakah relasi : fungsi atau bukan , kita dapat menggunakan Tes Garis Vertikal. Caranya yaitu cukup menggeser garis vertikal dari kiri ke kanan (atau sebaliknya) dan melewati garis relasi. Apabila garis vertikal tersebut memotong grafik di dua atau lebih titik yang berbeda, maka relasi tersebut bukanlah fungsi.
Kesimpulan :
Jadi, ada relasi yang merupakan fungsi dan ada juga relasi yang bukan merupakan fungsi. Setiap fungsi pasti relasi, setiap relasi belum tentu fungsi
 Sebuah pabrik pembuatan keripik tempe memiliki mesin yang beroperasi dengan mengubah 1 potong tempe bulat menjadi 6 keripik tempe. Pembuatan tempe dapat saja menghasilkan
Sebuah pabrik pembuatan keripik tempe memiliki mesin yang beroperasi dengan mengubah 1 potong tempe bulat menjadi 6 keripik tempe. Pembuatan tempe dapat saja menghasilkan
📥 Download LKPD
Kembali ke Menu Sebelumnya

