A. Lingkaran dan Busur Lingkaran
1. Lingkaran Lingkaran adalah tempat kedudukan titik-titik pada bidang datar yang berjarak sama terhadap satu titik tetap. Titik tetap tersebut dinamakan titik pusat (P). Jarak yang sama tersebut dinamakan jari-jari.

Rumus :
Luas Lingkaran = πr2
Keliling Lingkaran = 2πr
π = 3,14 atau \( \frac{22}{7} \)
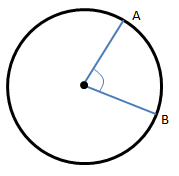 Keterangan:
Keterangan:
Rumus :
\( \frac{Panjang busur}{Keliling lingkaran}\) = \( \frac{Besar sudut pusat}{Sudut lingkaran} \)
\( \frac{Panjang AB}{2πr}\) = \( \frac{α}{360°} \)
Panjang AB = \( \frac{α}{360°} \) . 2πr
Soal Pemanasan:
1. Diketahui sudut pusat dan sudut keliling yang menghadap busur yang sama seperti gambar berikut:
Jika panjang ∠ APB merupakan sudut pusat yang menghadap busur AB dan ∠ ACB merupakan sudut keliling yang juga menghadap busur AB.
Jawab:
Panjang AB = \( \frac{α}{360°} \) . 2πr
-
= \( \frac{120°}{360°} \) . 2(\( \frac{22}{7} \))(21)
=\( \frac{1}{3} \) . (44)(3)
= 44
-
= \( \frac{135°}{360°} \) . 2π(12)
= \( \frac{9}{24} \) . 2π(12)
= 9π
Soal Pemanasan:
1. Perhatikan lingkaran berikut.
 Jika panjang PA = 21 cm dan besar ∠ APB = 120°, tentukan panjang busur AB!
Jawab:
Panjang AB = \( \frac{α}{360°} \) . 2πr
Jika panjang PA = 21 cm dan besar ∠ APB = 120°, tentukan panjang busur AB!
Jawab:
Panjang AB = \( \frac{α}{360°} \) . 2πr
 Jika panjang PA = 21 cm dan besar ∠ APB = 120°, tentukan panjang busur AB!
Jawab:
Panjang AB = \( \frac{α}{360°} \) . 2πr
Jika panjang PA = 21 cm dan besar ∠ APB = 120°, tentukan panjang busur AB!
Jawab:
Panjang AB = \( \frac{α}{360°} \) . 2πr
-
= \( \frac{120°}{360°} \) . 2(\( \frac{22}{7} \))(21)
=\( \frac{1}{3} \) . (44)(3)
= 44
-
= \( \frac{135°}{360°} \) . 2π(12)
= \( \frac{9}{24} \) . 2π(12)
= 9π






Tidak ada komentar:
Posting Komentar