C. Fungsi Invers

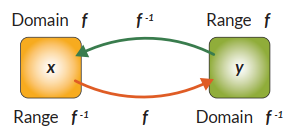
Ilustrasi 1
Jika kita memasukkan suatu kata dalam bahasa Inggris maka dapat dicari terjemahannya dalam bahasa Indonesia, begitu pula sebaliknya. Jadi proses mesin penerjemah bekerja secara bolak-balik.

Hal yang bekerja secara berkebalikan di kehidupan sehari-hari dalam bahasa matematika dapat disebut sebagai fungsi invers.

Secara konsep, menentukan fungsi invers dari fungsi asal dengan diagram panah memang lebih intuitif; dengan membalik arah panah. Namun, sering kali dijumpai bahwa fungsi asal dituliskan dalam bentuk persamaan matematis. Dalam kasus ini, cara untuk menemukan persamaan fungsi invers dari fungsi asal dapat dilakukan dengan cara berikut:

1. Ubah fungsi f(x) menjadi bentuk y.
2. Ubah persamaan menjadi x = . . .
3. Ubah variabel x menjadi f^-1(y) (x = f^-1(y))
4. Ganti variabel y menjadi x pada f^-1(y) sehingga diperoleh rumus fungsi invers f^-1(x)

Ilustrasi 2

Penjelasan:
Perhatikan gambar di atas:
f(x) = x - 2
y = x - 2 (ubah f(x) menjadi y)
x = y + 2 (ubah persamaan menjadi x = . . .)
f^-1(y) = y + 2 (ubah x menjadi f^-1(y)
f^-1(x) = x + 2 (ganti variabel x pada f^-1(y) dan dapatlah rumus fungsi invers f^-1(x))

Cakil (Cara Kilat):

f(x) = ax + b → f^-1(x) = \( \frac{x-b}{a} \)

\(f(x)= \frac{ax+b}{c} \) → f^-1(x) =\( \frac{cx-b}{a} \)

\(f(x)= \frac{ax+b}{cx+d} \) → f^-1(x) =\( \frac{-dx+b}{cx-a} \)

f(x) = axⁿ + b → f^-1(x) = \( ^n\sqrt\frac{x-b}{a} \)

f(x) = ^alog cx → f^-1(x) = \( \frac{a^x}{c} \)

f(x) = y → f^-1(y) = x

Soal Pemanasan:

1. Tentukan fungsi invers dari fungsi-fungsi berikut jika ada:
a. f(x) = 2x + 5
b. \(f(x)= \frac{2x-1}{6} \)
c. \(f(x)= \frac{2x+3}{x-5} \)
d. f(x) = \(^3\sqrt{x+2}\)
e. \(f(x)= \frac{5^x}{7} \)
Jawab:
a. f^-1(x) = \(\frac{x-5}{2} \)
b. f^-1(x) = \( \frac{6x+1}{2} \)
c. f^-1(x) = \( \frac{5x+3}{x-2} \)
d. f^-1(x) = x³ - 2
e. f^-1(x) = ⁵log 7x

1. Fungsi Injektif, Surjektif dan Bijektif (INSURBI)
Berdasarkan jenis relasinya, fungsi dibagi menjadi tiga jenis, perhatikan gambar dibawah ini!