B. Komposisi Fungsi

1. Penjumlahan dan Pengurangan Fungsi

Penjumlahan dua atau lebih fungsi dapat menghasilkan fungsi baru.
Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing D_f dan D_g. Maka penjumlahan (f + g) (x) = f (x) + g(x) menghasilkan fungsi yang baru dengan domain D_f ∩ D_f.
Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing D_f dan D_g. Maka penjumlahan (f - g) (x) = f (x) - g(x) menghasilkan fungsi yang baru dengan domain D_f ∩ D_f.

2. Perkalian dan Pembagian Fungsi

Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing D_f dan D_g. Maka perkalian (f · g)(x) = f(x) · g(x) menghasilkan fungsi yang baru dengan domain D_f dan D_g.
Pembagian dua fungsi \( \frac{f}{g}(x) \) = \( \frac{f(x)}{g(x)} \) secara umum belum tentu menghasilkan fungsi. Supaya \( \frac{f}{g}\) menjadi sebuah fungsi, pembagi g tidak boleh memiliki nilai 0. Dengan kata lain, \( \frac{f}{g}\) adalah fungsi dengan domain (D_f dan D_g) − {x| g(x) = 0}.

Soal Pemanasan:

1. Jika \(f(x) =\sqrt{x+3}\) dan g(x) = x + 3
a. Tentukan f(x) + g(x)
b. Tentukan domain dan range dari f(x) + g(x)
Jawab:
a. f(x) + g(x) = \(\sqrt{x+3}\) + x + 3
b. D_f : {x| x ≥ -3, x ∈ R}

D_g : {x| x ∈ R}
D_f+g = D_f ∩ D_g = {x| x ≥ -3, x ∈ R}
R_f+g = {x| x ∈ R}

2. Jika f(x) = x² + 2 dan g(x) = 2x - 5
   a. Tentukan f(x) - g(x)
   b. Tentukan domain dan range dari f(x) - g(x)
   Jawab:
   a. f(x) - g(x) = x² + 2 - (2x - 5)
   
   = x² + 2 - 2x + 5)
   = x² - 2x + 7
   
   b. D_f : {x| x ∈ R}
   
   D_g : {x| x ∈ R}
   D_f-g = D_f ∩ D_g = {x| x ∈ R}
   Nilai minimum fungsi kuadrat y = x² - 2x + 7 yaitu:
   y_min = \(- \frac{b^2-4ac}{4a} \)
   y_min = \(- \frac{(-2)^2-4(1)(7)}{4a} \)
   y_min = \(- \frac{-24}{4(1)} \)
   y_min = \(- \frac{-24}{4} \)
   y_min = 6
   
3. Jika f(x) = 3x² + 2x dan g(x) = 2x - 1
   a. Tentukan f(x) . g(x)
   b. Tentukan \( \frac{f(x)}{g(x)} \)
   

Jawab:
a. f(x) . g(x) = (3x² + 2x) . (2x - 1)

= 6x² - 3x² + 4x² - 2x
= 6x² + x² - 2x

b. \( \frac{f(x)}{g(x)} \) = \( \frac{3x^2+x^2}{2x-1} \)

3. Komposisi Fungsi
Komposisi Fungsi adalah fungsi yang melibatkan lebih dari satu fungsi atau penggabungan dari beberapa fungsi. Ketika ada suatu fungsi, kemudian dilanjutkan dengan fungsi lainnya maka akan membentuk suatu fungsi baru.
Operasi fungsi komposisi disimbolkan dengan "o" (dibaca: bundaran).

a. Jenis Komposisi Fungsi
Komposisi Dua Fungsi

(f o g)(x) = f(g(x))

(g o f)(x) = g(f(x))

Komposisi Tiga Fungsi

(f o g o h)(x) = f(g(h(x))

Komposisi Lebih dari Tiga Fungsi

(f o g o h o i)(x) = f(g(h(i(x)))

Ilustrasi 1

Jika Padi = f(x) dan Beras = g(x) merupakan dua fungsi, maka komposisi keduanya dinyatakan dengan (g o f)(x) = g(f(x)) = Nasi

Ilustrasi 2

Jika Mie Instan = f(x) dan Telur = g(x) merupakan dua fungsi, maka

(f o g)(x) = f(g(x)) → akan menjadi mie telur

(g o f)(x) = g(f(x)) → akan menjadi omlet

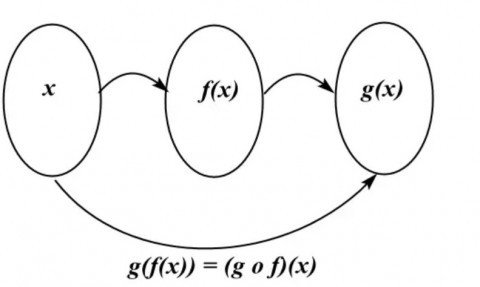
Komposisi dua fungsi dapat dipahami melalui diagram panah berikut:

b. Sifat-sifat Komposisi Fungsi
1) Tidak Komutatif → (f o g)(x) ≠ (g o f(x)
Contoh:
Jika f(x) = x + 2 dan g(x) = 2x, maka (f o g)(x) = 2x + 2, sedangkan (g o f)(x) = 2x + 4.
2) Asosiatif → (f o (g o h))(x) = ((f o g) o h)(x)
Contoh:
Jika f(x) = x + 1, g(x) = 2x, dan h(x) = 3, maka (f o (g o h))(x) = (f o (2*3))(x) = (f o 6)(x) = 6 + 1 = 7, dan ((f o g) o h)(x) = ((x + 1) o 2x)(3) = ((3 + 1) o 6)(3) = 7.
3) Identitas → (f o I)(x) = (I o f)(x)
Contoh:
Jika f(x) = 2x + 1, maka (f o I)(x) = (2x + 1) o x = 2x + 1, dan (I o f)(x) = x o (2x + 1) = 2x + 1.

Soal Pemanasan:

1. Jika \(f(x)= \frac{1}{4x^2+1} \) dan g(x) = 2x² + 1, tentukan:
   a. (f o g)(x)
   b. domain dan range (f o g)(x)
   c.(g o f)(x)
   d. domain dan range (g o f)(x)
   Jawab:
   a. (f o g)(x) = f(g(x))
   
   = f(2x² + 1)
   =\( \frac{1}{2(2x^2+1)+1} \)
   =\( \frac{1}{4x^2+2+1} \)
   =\( \frac{1}{4x^2+3} \)
   
   b. domain dan range (f o g)(x) adalah semua bilangan riil.
   c. (g o f)(x) = g(f(x))
   
   = g(\( \frac{1}{2x+1} \))
   = 2(\( \frac{1}{2x+1})^2 \) + 1
   = \( \frac{2}{4x^2+4x+1} \) + 1
   d. domain dari (g o f)(x) adalah semua bilangan riil kecuali \( \frac{1}{2} \), rangenya ialah semua bilangan riil.
   
2. Diketahui f(x) = 2x + 1 dan (f o g)(x) = 10x + 7. Tentukan g(x)!
Jawab:
(f o g)(x) = 10x + 7
f(g(x)) = 10x + 7
2.g(x) + 1 = 10x + 7
2.g(x) = 10x + 7 - 1
2.g(x) = 10x + 6
g(x) = \( \frac{10x + 6}{2} \)
g(x) = 5x + 3

3. Diketahui g(x) = 5x + 3 dan (f o g)(x) = 10x + 7. Tentukan f(x)!
Jawab:
(f o g)(x) = 10x + 7
f(g(x)) = 10x + 7
f(5x + 3) = 10x + 7
Misalkan 5x + 3 = a, maka \(x= \frac{a-3}{5} \) (ubah persamaan menjadi x = ...)
f(a) = 10(\( \frac{a-3}{5} \)) + 7 (substitusi x dengan \( \frac{a-3}{5} \))
f(a) = 2(a - 3) + 7
f(a) = 2a - 6 + 7
f(a) = 2a + 1
f(x) = 2x + 1

📥 Download LKPD Kembali ke Menu Sebelumnya